Hao Peng, Ph.D.

Research interests: Acoustic Metamaterial Design, Oscillating Heat Pipes (OHPs), Metallic Additive Manufacturing, Material Point Method (MPM), CFD Modeling of Airfoils, Monte Carlo (MC) Simulation for Phonon Transport

Acoustic Metamaterial Design (to top)

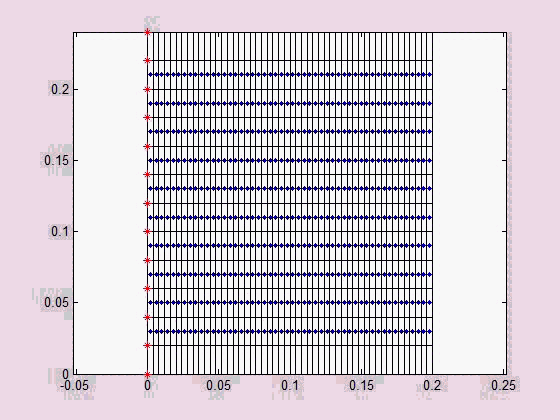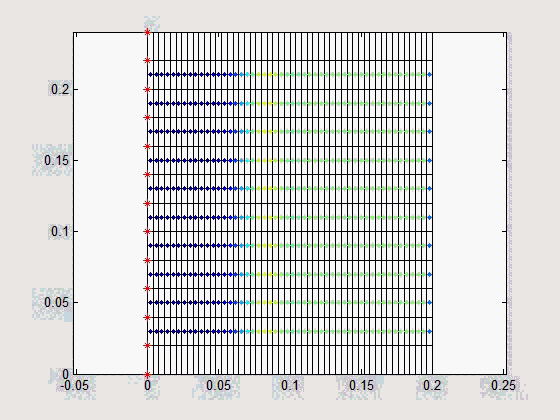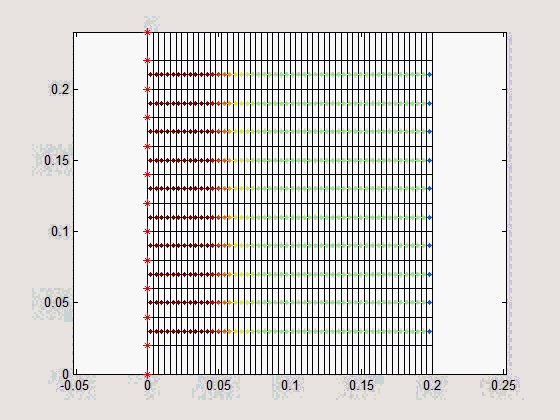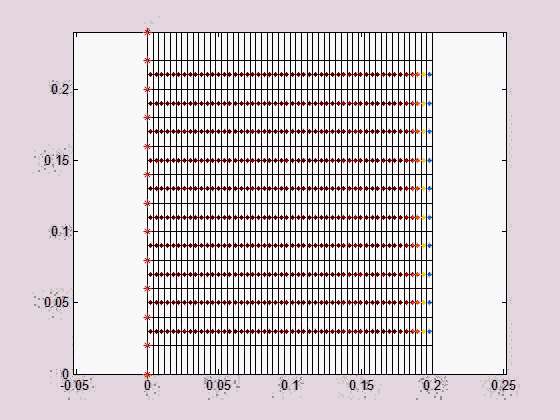
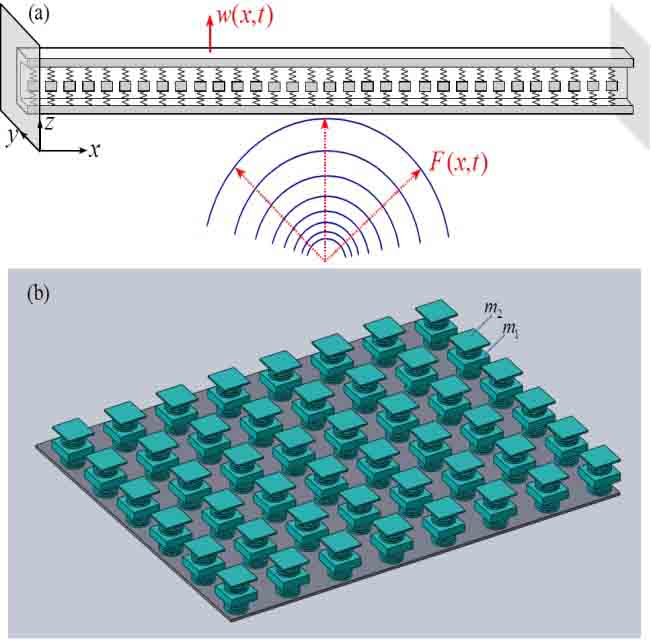
Acoustic metamaterials are intelligent material structures that can attenuate/stop or guide an elastic wave propagating along a desired path by employing the resonance of the integrated local subsystems. If elastic waves are not allowed to propagate within a successive frequency band, the frequency band is called stopband. Figure (a) shows a single-stopband acoustic metamaterial beam and Fig.(b) shows a two-stopband acoustic metamaterial plate (local subsystems denoted by m1 and m2). The two stopbands of the metamaterial plate is manifested by the dispersion relations shown in Fig. (c). Both metamaterial structures use mass-spring subsystems as vibration absorbers.

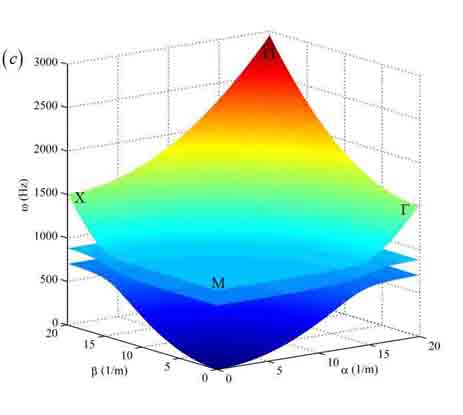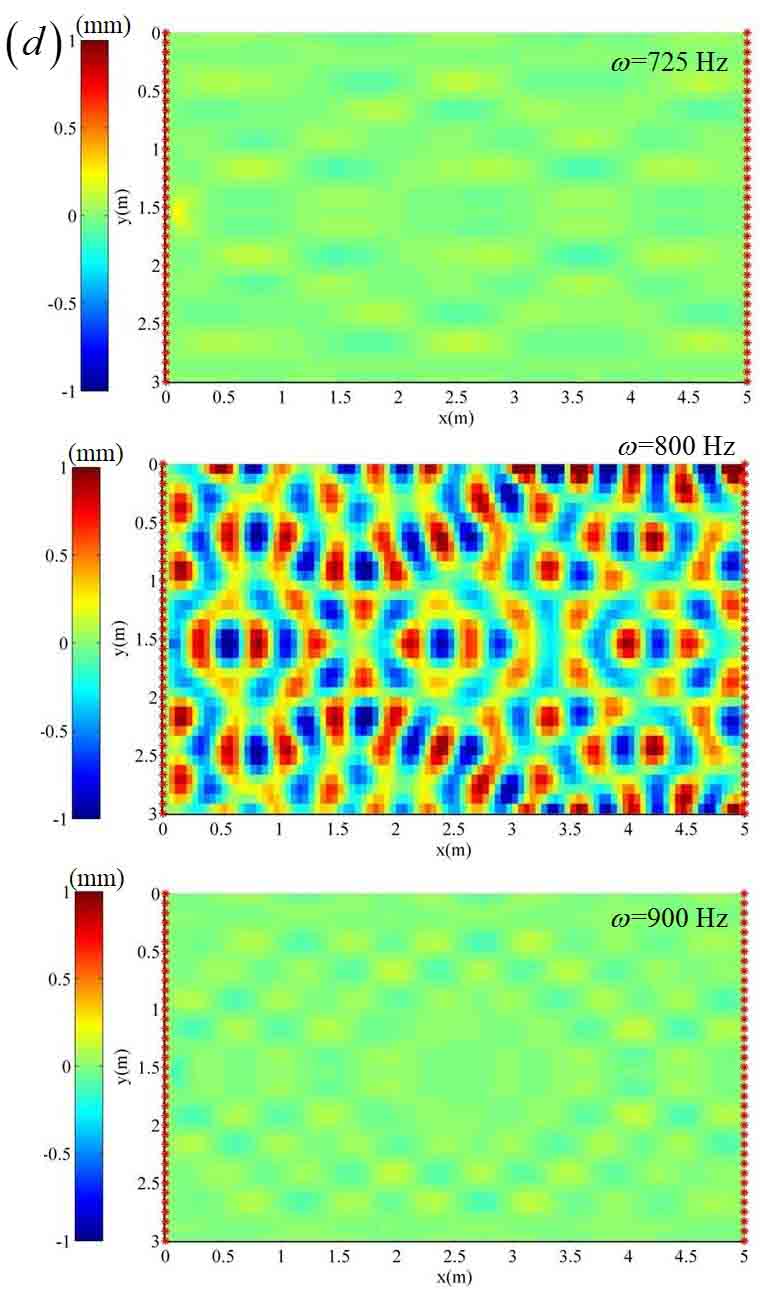
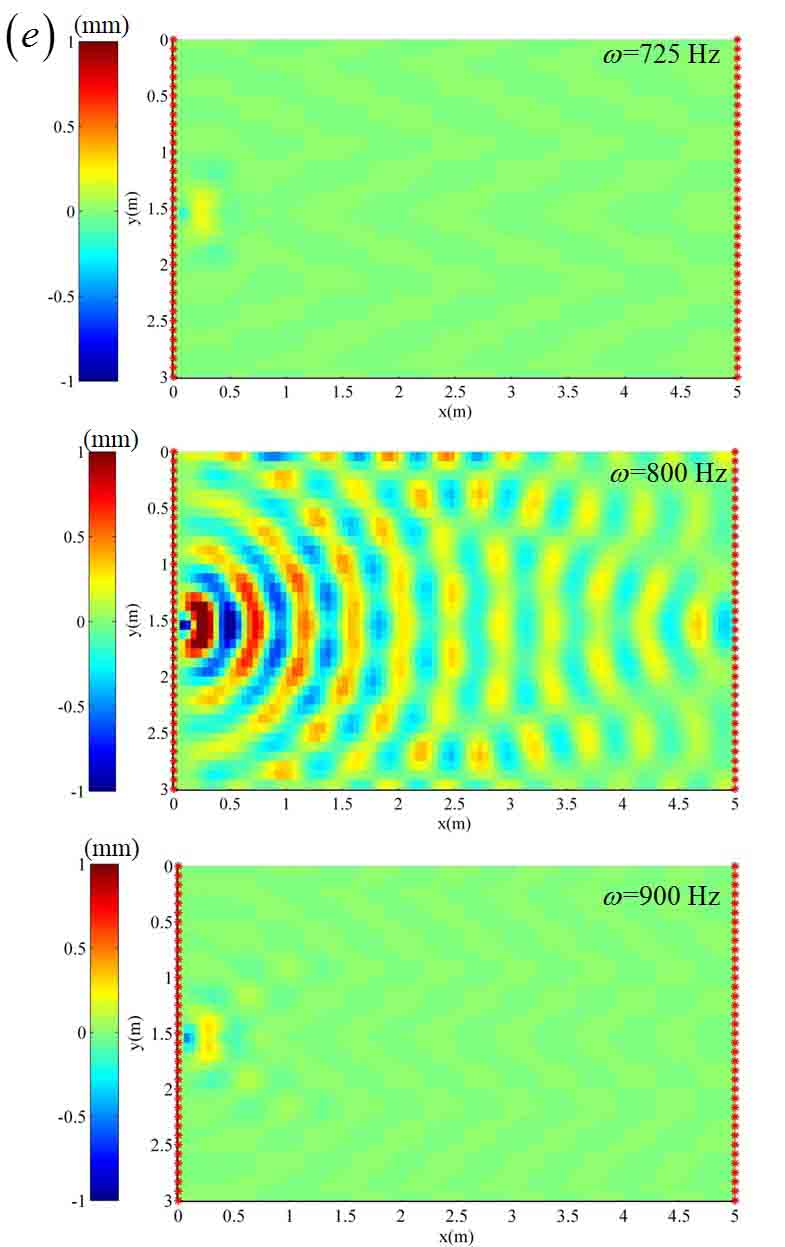
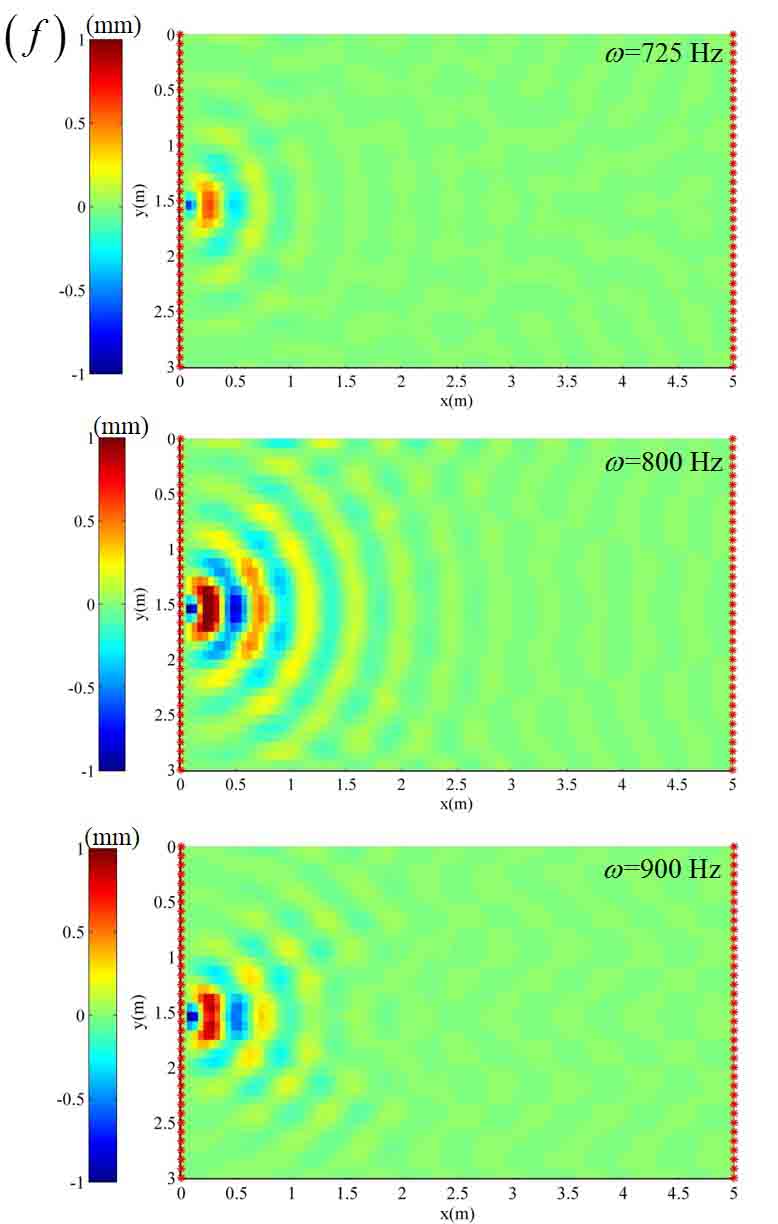
Figure (d-f) show the steady state vibration pattern of a two-stopband acoustic metamaterial plate with different damping for m2 under three different vibration frequencies (two frequencies in the two stoptands, respectively, and one in between). Each stopband's bandwidth can be increased by increasing the absorber mass and/or reducing the isotropic plate's unit cell mass. Moreover, a high damping for m2 can help combine the two stopbands into a wide one as shown in Fig. (f).

Publications:

Oscillating Heat Pipes (OHPs) (to top)

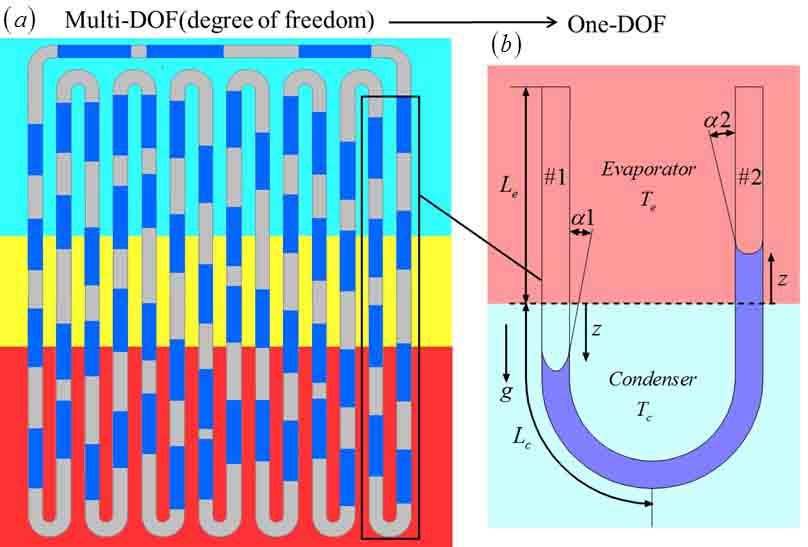
OHPs are promising heat dissipation devices for modern electronic systems. However, accurate modeling of OHPs is hard because OHPs are essentially complicated multiphysics device, which incorporates mechanical dynamics, convective heat transfer, thin film evaporation/condensation into a single problem. Figure (a) shows a typical OHP and Fig. (b) is its one-DOF working unit. The red, cyan and yellow backgrounds in Fig. (a) represent evaporator, condenser and adiabatic area, respectively. The liquid slugs in the capillary tube are in blue and the vapor slugs are in grey.

The modal analysis of an OHP reveals its inherent working mechanism. The zero-frequency movement (rigid-body movement) is crucial because it initiates and sustains the two-phase flow, carrying heat continuously from the evaporator to the condenser. Although the high-frequency modes, e.g., mode #3, do not contribute to the circulation of the flow, high-frequency oscillation of liquid slugs creates high velocity/temperature gradients and significantly increases convective heat transfer between the liquid slugs and the tube wall. Besides, the trailing edge of the quick-moving liquid slugs leave thin films on the tube wall and facilitate the phase-change heat transfer. In conclusion, an appropriate combination of different modes guarantees the high heat transfer capability of an OHP.

mode #1 f=0Hz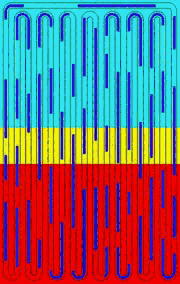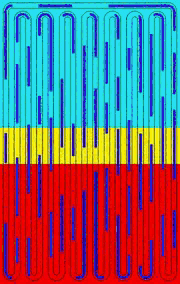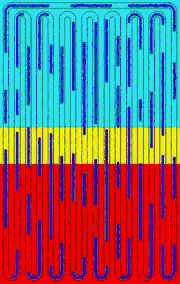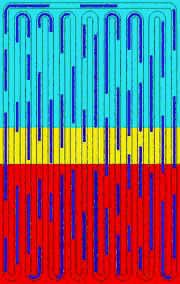

mode #3 f=5.03Hz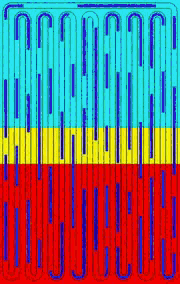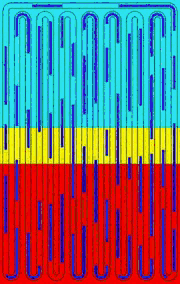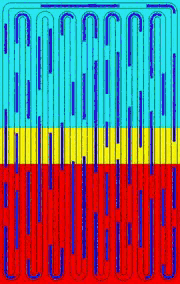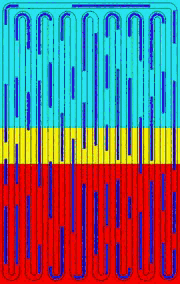

mode #1+#3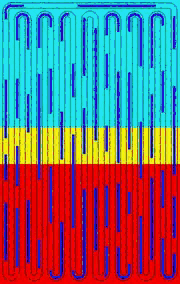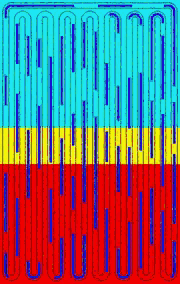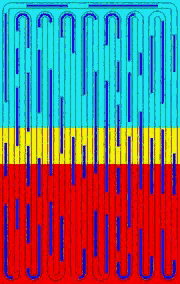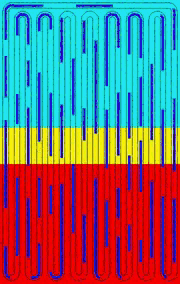

The heat transfer of an OHP comes from two parts, convective heat transfer and phase-change heat transfer. The phase-change heat transfer accounts for less than 10% of the total heat transfer, which is consistent with the experimental data in literatures. Despite of the low percentage of phase-change heat transfer, the high-pressure vapor generated during the phase change process provides driving force for the oscillating flow. When the external heat power increases, the phase-change heat transfer increases also, which makes the heat tranfer capability of an OHP almost proportional to the heat input.

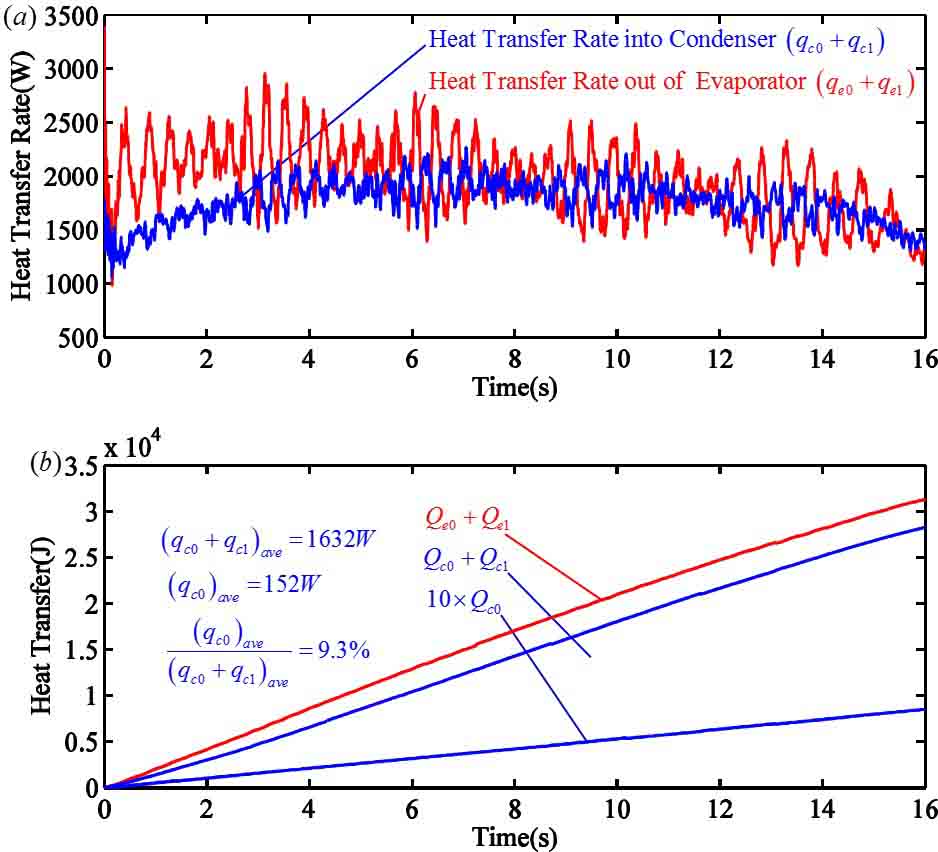Publications:

Metallic Additive Manufacturing (to top)

Metallic additive manufacturing (AM) processes, including selective laser sintering (SLS), selective laser melting (SLM), electron beam melting (EBM) and direct metal laser deposition (DMLD), are inherently multiphysical processes. A reliable model of AM should consider laser/electron beam absorption, heat conduction into the metal powder bed, convection and radiative heat transfer into the inert gas phase, phase change of metal powders, Marangoni convection in the melt pool, balling effect due to Plateau-Rayleigh instability, the dynamic motion of metal powders and the residual stresses after manufacturing. The state-of-the-art modeling methods of AM range from traditional finite element (FE) or finite volume methods, to novel approaches such as volume of fluid method (VOF), level-set method, lattice Boltzmann method (LBM) and discrete element method.

Figures (a) and (b) show a FE model developed by Chou and et al. to simulate the transient heat transfer in a part during EBM subject to a moving heat source. The porous powder bed was modeled as a continuum body with porosity-dependent physical properties. The region with temperature higher than the melting point was assumed to be the melt pool region.

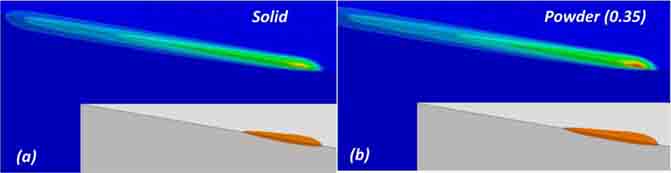
Cheng B, Price S, Lydon J, Cooper K, Chou K. On Process Temperature in Powder-Bed Electron Beam Additive Manufacturing: Model Development and Validation. Journal of Manufacturing Science and Engineering. 2014;136:061018.

Figures (c) and (d) show the melting and resolidification processes in an EBM model developed by Korner and et al with LBM. The powder bed was modeled as discrete metal powders. The complex interaction between gas, liquid and solid phases was captured by incorporating the VOF free surface method into LBM. The wetting and shrinkage effect were well modeled as shown in the figures.

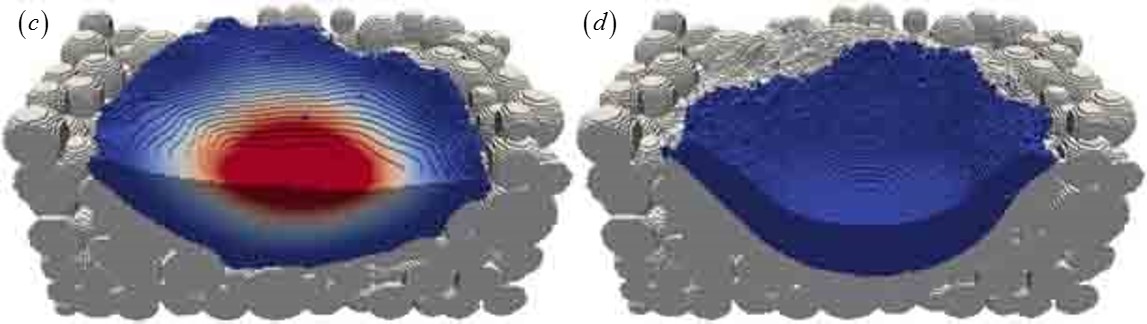
Ammer R, Markl M, Ljungblad U, Körner C, Rüde U. Simulating fast electron beam melting with a parallel thermal free surface lattice Boltzmann method. Computers & Mathematics with Applications. 2014;67:318-30.

Figures (e) and (f) show the temperature and velocity field in a DMLD process modeled by Liou and et al. The free interface between liquid and solid phases was captured by VOF method, and conservation equations were solved to obtain the temperature and velocity field.

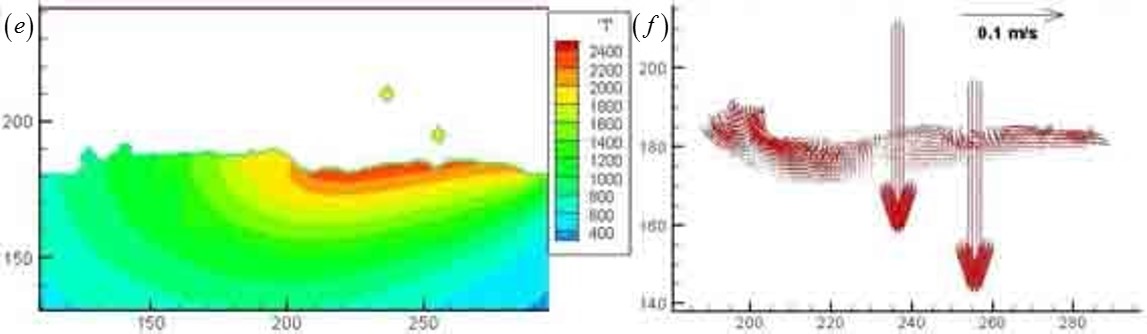
Fan Z, Liou F. Titanium Alloys - Towards Achieving Enhanced Properties for Diversified Applications. InTech; 2012.

Material Point Method (MPM) (to top)

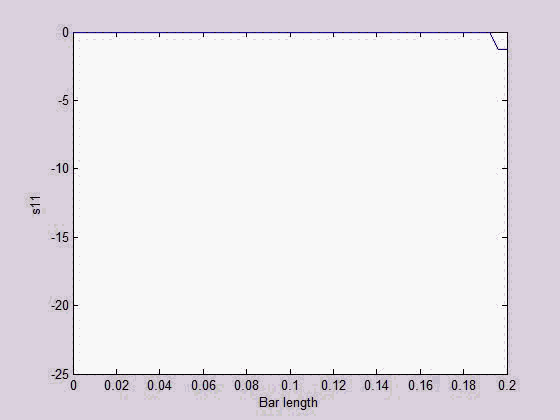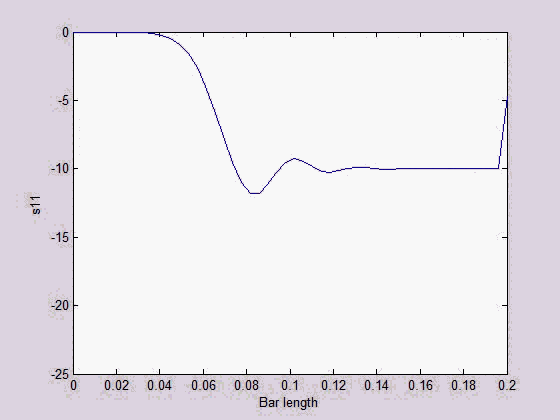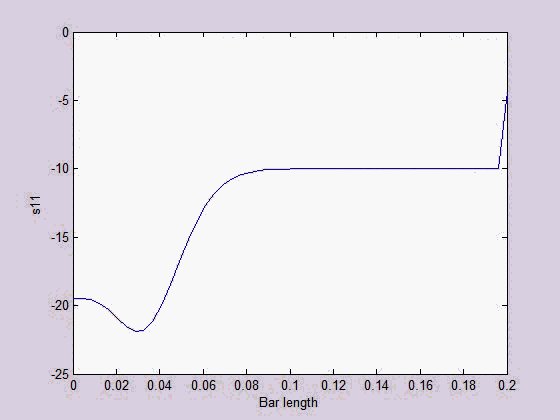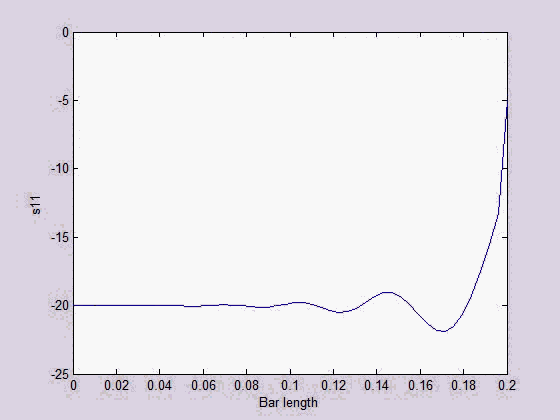
MPM is a particle-based meshfree numerical method which is useful for large material deformation simulation. A bar structure subject to extension force was modeled with a 2D MPM. Both the normal and shear stress wave propagations were captured.

Bar modeled by 2D MPM

Axial normal stress wave propagation

CFD Modeling of Airfoils (to top)

Two adjacent airfoils are modeled with upwind algorithm. The conservation equations of mass, momentum and energy for compressible air are solved simultaneously with Matlab. The shock wave can be well captured and the steady-state velocity, density and pressure fields are computed.

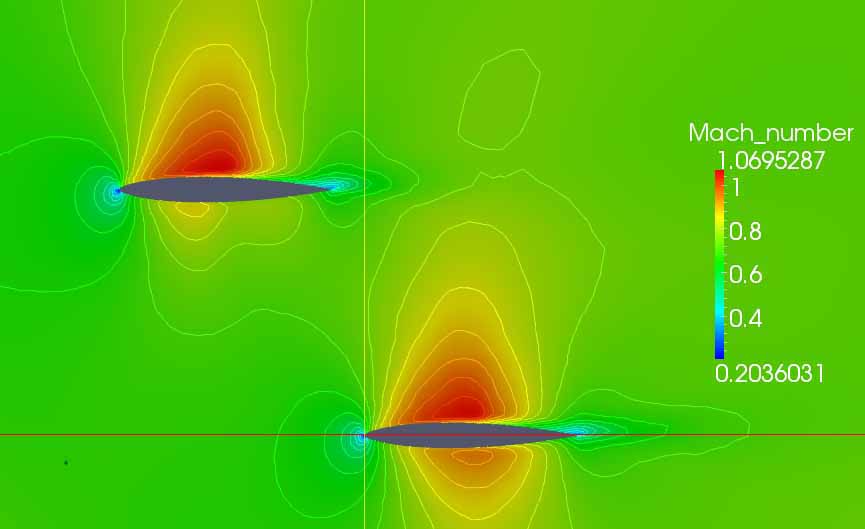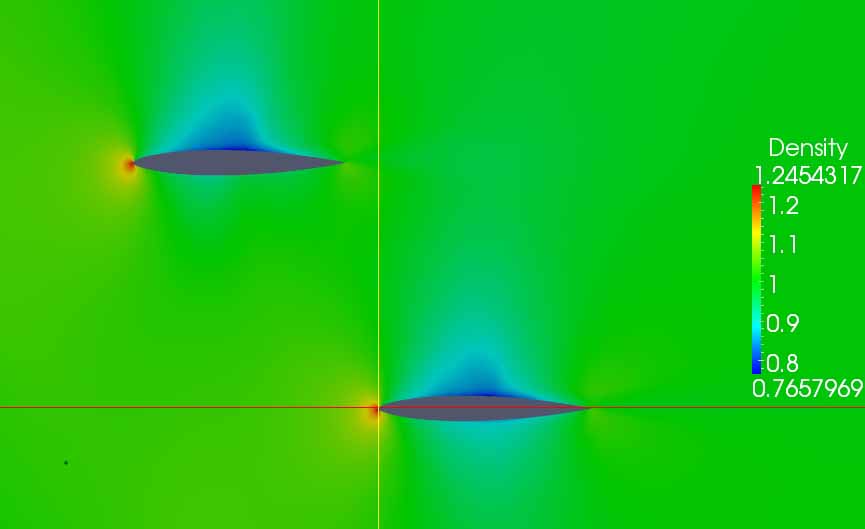Monte Carlo (MC) Simulation for Phonon Transport (to top)

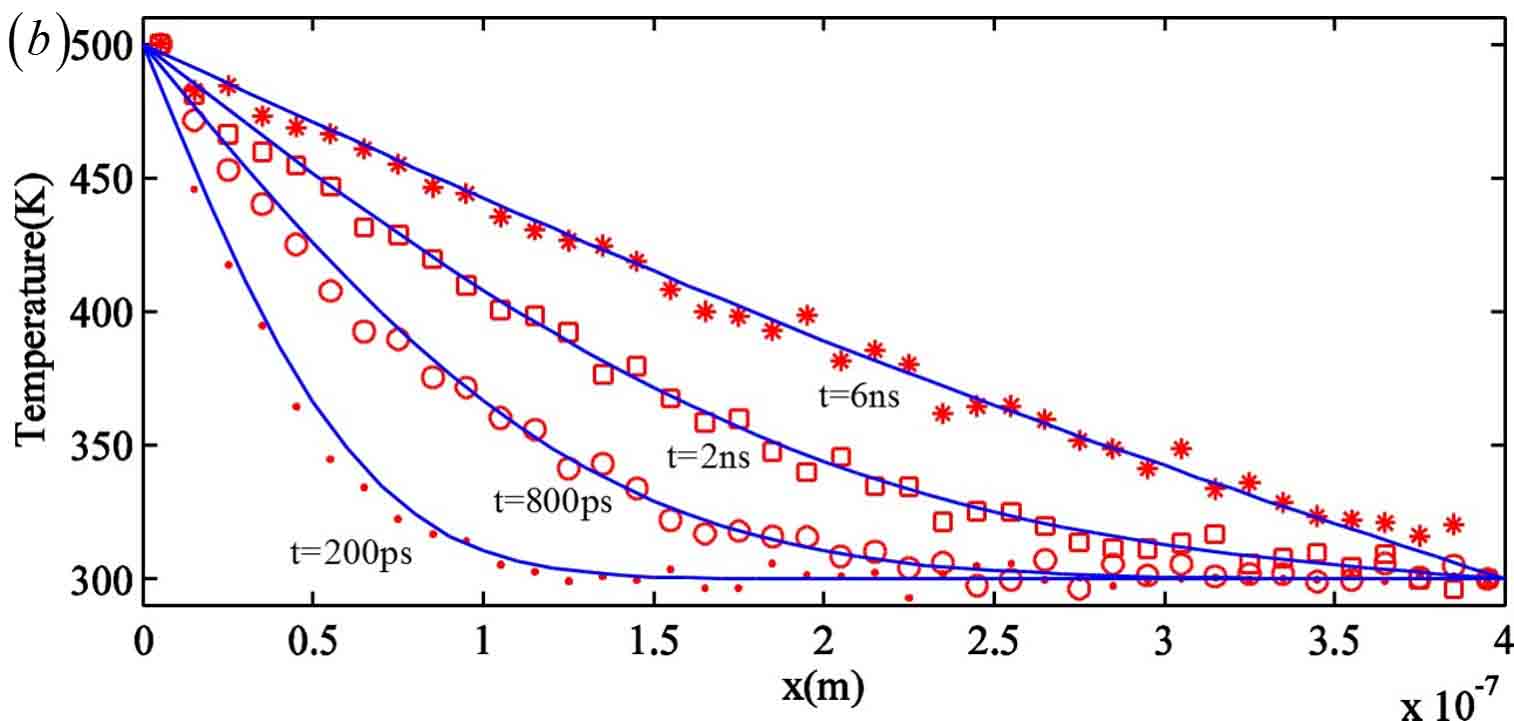
MC method, a method using mathematical sampling, is usually used in complex problems which are intractable with conventional ways. Here, the heat transfer along a nanowire is modeled with MC method. At nanoscale, the well-known Fourier's law of heat transfer breaks down and heat is transferred in particle-like energy quanta, which are called phonons. Figure (a) shows three cells with edge length 10nm filled with randomly distributed phonons. In real simulation, 40 cells are used to model a nanowire of length 400nm. The results are shown by red symbols in Fig. (b) and compared against results from Fourier's law which denoted by blue lines. At large time scale (>800ps), the results from MC simulation well fit to the results from Fourier's law. However, at short time scale, e.g., 200ps, the results significantly deviate from the Fourier's law. The deviation results from the ballistic heat transport at short time scales.

Web Counter

free hits
WebTracking